Quick Reference

Tool 1: The Cost Per $1,000 financed table 
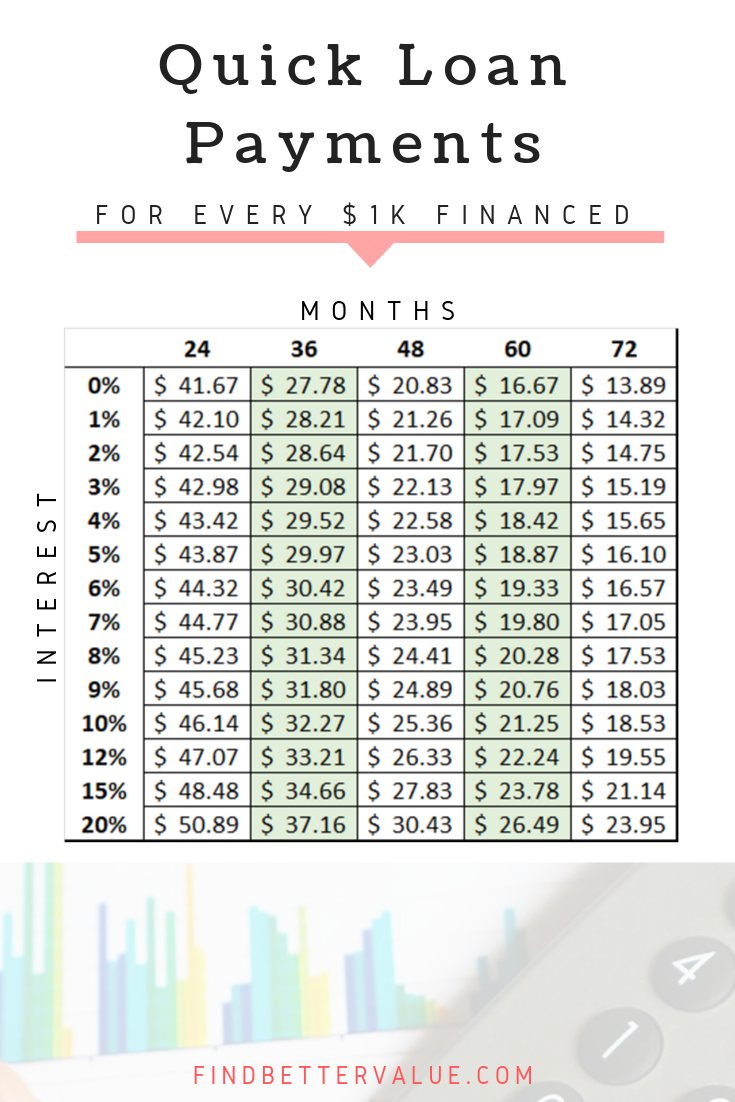
Table of monthly payments per $1000 of principal
Tip 1: Quickly estimate a payment without any tools or reference

Know Your Payments Quickly

Knowing how to calculate rough payments using the cost per $1,000 method can help you in a lot of different ways.  It can help you determine what your payment should be when shopping for a car, it can help you get an idea of what a payment would be for an expensive item like a boat or house, and more importantly, it can help you negotiate good terms.

Using the Cost per $1,000 method gives you the power to quickly determine a monthly payment.  The actual formula and calculations for determining montly financed payments can be very difficult and extensive to calculate.  Fortunately, you don’t have to be a math wizard and using methods like the cost per $1,000 can save you time.

There are some simple ways to quickly make the calculation to get an approximate monthly payment.  In fact, you have almost certainly heard of them in car financing ads “16.67 per $1,000 financed” or “$17.09 for every $1,000 financed” or other such terms.

So here are some quick ways and tools to help you make your monthly payment calculation on the fly.

Tool 1: The Cost Per $1,000 financed table 

This one is a great fast and simple reference tool that you can keep with you.  I have included a pintrest graphic to pin or post to your facebook account for quick reference.  You can even print out the montly payment table below and keep it in your wallet.

The cost per $1,000 financed method simply helps you break down how much a monthly payment would be for every $1,000 borrowed at a given interest rate.  This makes it really easy to know an approximate payment.

Table of monthly payments per $1000 of principal

Here is how to use it:

You need three pieces of information: Your estimated interest rate, the price of the item, and the length of the loan you are looking at.

1. Know the approximate interest rate that you are being offered or that you think you will qualify for.  In this example let’s say it is 5%.
2. Calculate your price of the item: let’s say $23,000
3. Determine the length you will be going for on the loan: Lest say 60 months
4. Now simply find the closet interest rate and long term combination and find the dollar amount per $1,000 financed.
5. In our example, it is $18.87.  Since you will be going for $23,000 all you have to do is multiply $18.87 X 23 = $434.01.
6. That is it, your estimated payment is $434.01.

If you ever see $16.67 per $1,000 advertised for a car, it is always the terms for 0% financing for 60-months.  A common offer at many dealerships.

If your variables do not equal any of the amounts then just approximate your payment be trying to find the right mid-points between two amounts.

Remember, most loans should be even year terms.  If you see odd term loans, the primary reason it is done is to make it harder to shop competitive offers or slightly lower payments to make their offer look better.

Tip 1: Quickly estimate a payment without any tools or reference

This might come in handy in discussions, brainstorming, or quick calculations you might be trying to figure out.

If you want a very rough answer quickly then you can simply do the following:

1.       Divide the loan amount by the term (or your best approximation)

2.       This is a bit tricky but you can get the hang of it: Every 1% jump in interest adds about $.45 per 1,000 financed.  So multiply .45 x interest rate x the number of thousands.

Let’s do a quick example on the same numbers from above:

$2300/60 = 383.33

Now multiply .45*5 = $2.25 X 23 = $51.29

Now add the two together: $$434.62 Close to the first example.

The best secret to using this method is to remember the $.45 and then use round numbers for easy calculations and approximate the rest.  The key with this method is not to be so accurate as it is to just be in the ballpark.  If accuracy is needed, use a calculator.

Tip 2: What do I use to understand monthly payments?

What I use really depends on what I need the information for.  For example, I might be browsing a rental property to buy and want to approximate what a monthly payment would be based on a certain down payment to quickly see if it would cash flow.

For something like that, I use loans I already have that are similar and adjust them by percentages to approximate the payment.  If I want an accurate dollar amount I would use any of the available free calculators online.

If I really want to dig into the numbers, then I would model them out in a spreadsheet and add all the nuances and sensitivity analysis to help me understand what factors are going to help me get the best deal and make the numbers work.

If I am at a car dealership negotiating a car, I will have a cheat sheet like the table I have provided to use as a quick sanity check the dealer is not adding in any extra costs.

There are many different ways to use the various tools, the most important thing is that you use them!

Be smart with your money and understand the cost of money!

Understanding the cost of credit or what your payments will be helps you in all big purchases and also can even help you in small purchases if using a credit card.

If you calculate the cost of a simple small item using a credit card at 25% interest, you probably would not make the purchase until you could pay cash.

Understanding how payments are calculated also opens the door to understanding how much interest you will pay.  It helps you also understand different options like leasing vs. buying, home financing, Impact of Investing in your IRA, and so many other things.

Don’t limit yourself to just understanding how to calculate payments, expand to all the other areas and you will become much smarter with your money.

If you have any useful tips on how to calculate approximate payments quickly, please post them in the comments below.